拓扑相变
在数学中,拓扑是只考虑几何图形或空间中的位置关系,在经过形变后一些性质仍然保持不变的学科。一个常见的例子是甜甜圈和马克杯,它们都只有一个贯穿的孔洞,可以通过连续的形变的得到,亏格(genus)都为1(亏格n指沿闭简单曲线切开但不切断曲面的最大曲线条数)。这里的亏格,也可理解为一个几何形状所具有的孔洞数。如图1,描述四种不同的拓扑形状。
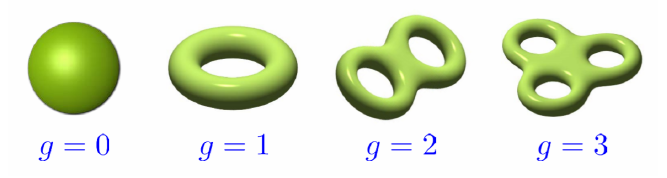
一般地,可以用欧拉示性数\(\chi=2-2g=\mbox{顶点数}-\mbox{边数}+\mbox{面数}\)来描述,\(g\)为亏格。例如一个四面体和一个球体,互相通过连续形变可以得到,那么二者欧拉示性数就是相同的 而更一般的情况下,需要使用Gauss-Bonnet定理:几何形状的拓扑数\(\chi(M)=\frac{1}{2\pi}\int_M R(x) d^2x\),其中\(R(x)\)为流形\(M\)上\(x\)处的高斯曲率。
这些,都是研究在实空间的拓扑结构。引入到能带理论,则是在\(k\)空间中的拓扑结构。由于周期性,只需要关注一个布里渊区。\(k=k+G\),一个\(n\)维的布里渊区可以用一个\(n\)维的面包圈结构表示。例如二维下可以将一个布里渊区卷曲接合成一个环面(\(T^2\))
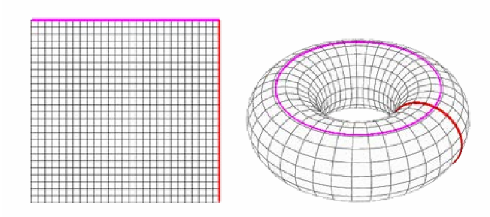
在动量空间里,类比引入一个拓扑数——Berry相位\(\gamma\)。
对任意波函数\(\ket{\phi(t)}\),在\(k\)空间演化过程中相因子变化来源于两部分: \[\ket{\phi(t)}\rightarrow e^{i\left[\theta(k)+\gamma(k)\right]}\ket{\phi(t)}\] \[\alpha(k)=\theta(k)+\gamma(k)\] 其中: \[\theta(k)\equiv -\frac{1}{h}\int_{k_{initial}}^{k_{final}}E_n(k)\cdot dk\]为动力学部分, \[\gamma(k)\equiv\oint_C\bra{u(k)}\nabla_k\ket{u(k)}\cdot dk\]为几何相位部分。
因为bloch函数是定态波函数,动力学部分在该闭合路径上积分为零。波矢演化时相对相位变化\(d\gamma\)为 \[e^{id\gamma}=\dfrac{\braket{u(k)|u(k+dk)}}{|\braket{u(k)|u(k+dk)}|}\] 可得到\(d\gamma=i\bra{u(k)} \nabla_k\ket{u(k)}\cdot dk=A(k)\cdot dk\)。其中\(A(k)\)为Berry Connection,是规范依赖的。对其取旋度可得到Berry curvature,具有规范不变性。\[\nabla \times A(k)=\nabla\times i\bra{u(k)} \nabla_k\ket{u(k)}\] 现在再求Berry Curvature对参数空间的围道积分,得到 \[\gamma=\oint_C\nabla\times A(k)\cdot d\mathbf{K}\] 一般我们称之为Chern数或TKNN数(\(\mathbb{Z}\))
拓扑超导体
拓扑类型的分类方法
十重分类
通过同伦群计算得到拓扑十重分类的周期表,根据体系所具有的对称性:time-reversal symmetry(T)、charge-conjugation symmetry(or particle-hole)(C) 以及 sublattice symmetry(or chrial)(S)查表得到对应维度的拓扑类型。
离散对称性(时间反演对称性、粒子空穴对称性、手征对称性):
(1). 时间反演对称性\(T = U_{T}K\),其中\(K\)是复共轭算符\(U_T\)是幺正算符。其满足\(T^2 = \pm 1,TH = HT\)。
(a).\(T^2 = 1\):保证波函数可以取为实数。 e.g. \(T = K, T = \sigma_x K, T = \sigma_z K\)
(b).\(T^2 = -1\):在此条件下由\(|\phi\rangle,T|\phi\rangle\)是哈密顿量\(H\)的具有同一本征值的简并态。Kramers简并 e.g.\(T = \mathrm{i} \sigma_y K\)
(2). 粒子空穴对称性\(C = U_{C}K\),其满足\(CH = -HC\),同理有\(C^2 = \pm 1\)
(a).\(C^2 = 1\)如:\(C = \tau_x K\),\(C^2 = -1\)如:\(C = \tau_y K\)
(3). 手征对称性
(a). \(S = CT = U_C U_T^{*}\)。
(b). 存在\(T\)对称和\(C\)对称,一定存在\(S\)对称。存在\(T\)和\(S\)一定存在\(C\),存在\(T\)和\(C\)一定存在\(S\) 由此给出了对称性存在的类型的限制。
(4). 十重对称性:
(a).所有对称性都没有:1
(b).具有C对称性和T对称性,其一定具有S对称性。根据\(T^2 = \pm 1, C^2 = \pm 1\): 4
(c).C对称性和T对称性只具有一种:4
(d).只具有S对称性: 1
加起来\(1+4+4+1=10\)
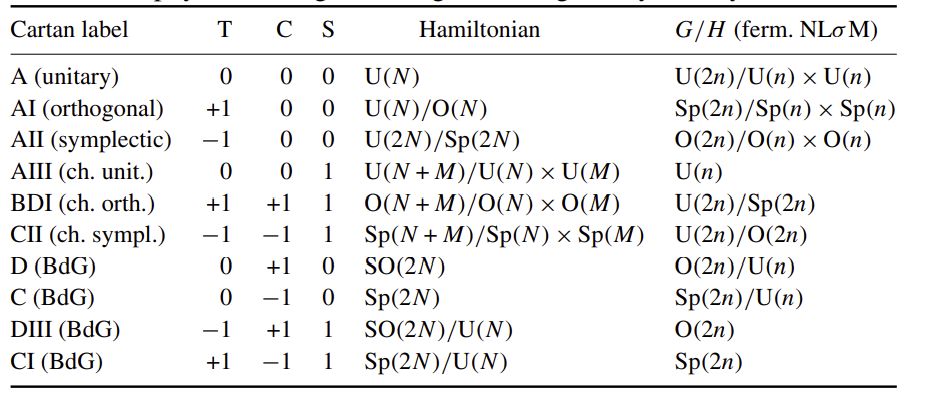

Wilson loop
通过DFT计算,用wilson loop来区分拓扑类型(ref: Yu Rui)。
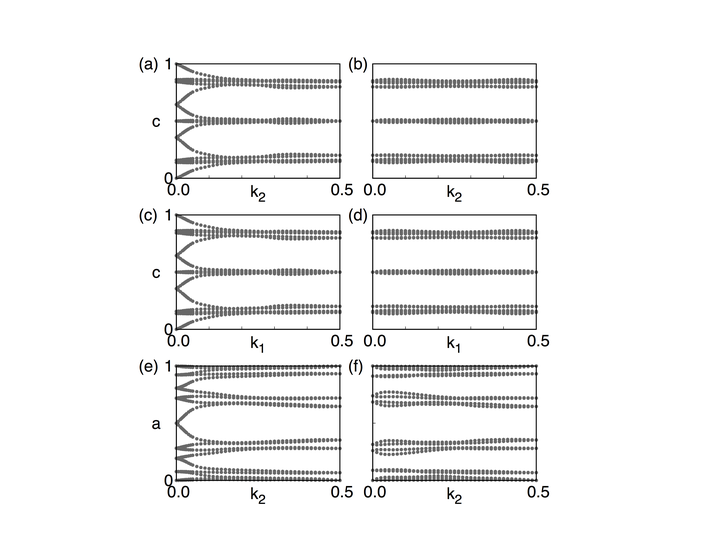
通常所说的\(\mathbb{Z}_2\)数是在一个2维闭合曲面内定义的一个拓扑数,比如在\(k_x =0\)的平面内(由于布里渊区的周期性,所以有闭合曲面的概 念)。这里a-f六幅图分别画的是在 \(k_1=0.0\)、\(k_1=0.5\)、 \(k_2=0.0\)、\(k_2=0.5\)、 \(k_3=0.0\)、\(k_3=0.5\)平面内的Wilson loop演化图,从这些演化图中可以知道每一幅图的\(\mathbb{Z}_2\)数。规则是:在图中画一条从左到右的曲线,数这条曲线和图中曲线的交叉点个数。如果交叉点个数为奇数,那么\(\mathbb{Z}_2\)数为1,拓扑非平庸;如果为偶数,那么\(\mathbb{Z}_2\)数为0,拓扑平庸。
TSC的理论基础
需要补充
时间反演对称破缺
受时间反演保护的
TSC 最简单的模型是具有 p 波配对的无自旋(单自旋)费米子 Kitaev 链。这个模型不具有时间反演不变性,根据拓扑 Z 不变量分类属于 BDI 类 .
QSH Phys. Rev. Lett. 95, 226801 (2005)
实验检测
拓扑超导和普通超导体的最大区别在与边界态是否存在。如何确定边界态的存在?可以利用超导体的输运性质:Josephson节、Andreev 反射。
由于Andreev反射,一维拓扑超导体和正常金属构成的Josephson结在零偏压的时候,微分电导率是一个量子化的值\(G(0)=2ne^2/h\)(\(n\)为边界上的Majorana零模的数目)。只要超导体的非平凡拓扑性质不改变,这个量子化的值将不随超导体和金属的参数以及它们之间的界面隧穿势垄的改变而改变,但是一旦拓扑性质改变,它将不再量子化,在隧穿极限下,即隧穿势全非常大的情况下,此时它的值将趋于零。因而,很明显,\(G(0)\)的量子化与否直接对应超导体是否拓扑非平凡。
补充其他方法
进展
基于近临效应
理论基础L. Fu, C. L. Kane, Phys. Rev. Lett. 100, 096407 (2008).
基于近临效应的复合体系,一般选择的是常规超导体,原因在于高温超导体的相干长度太小, 界面耦合的公度性差。
Rashba 原子线缺陷
Rashba 自旋轨道耦合、s 波超导、磁塞曼耦合结合会产生一维奇数宇称的 TSC
PRL104.040502.2010 Jay D. Sau,Phys. Rev. Lett. 105, 077001(2010)., Phys. Rev. Lett. 105, 177002 (2010).
Rashba 原子线缺陷(RALD )

生长的原子线缺陷对应于 Fe 平面上方缺失的一条 Te/Se原子线,缺失原子打破了下面的铁原子作为中心的反转对称性,产生了大的 Rashba 旋轨耦合 \(\alpha_R\)。为了强调这一性质,将后者称为 Rashba 原子线缺陷 (RALD)。文中展示了由于原子缺失导致的反转对称性破缺和电荷转移,引至占据受主杂质能带和穿过线缺陷的临近电子混合宇称的自旋单态、三态库珀配对。
半导体-超导体异质结
这是研究很多的一个方向。rashba 旋轨耦合的近邻半导体是比较成功的一类平台,但是需要试加较大的磁场以达到拓扑状态。这对超导电性、器件化以及应用场景都是不利因素。用铁磁层代替外磁场的想法下,发展了加入FM绝缘层的结构。(这里可以对比一下RALD平台)
(a)InAs/EuS/Al heterostructures:
计算说明两种不同的叠层结构,并可以得到何种结构对应的拓扑区域是否存在
表面金属线
纳米线方案的实验工作已经发现了在混合超导体-半导体纳米线器件的隧道光谱研究中出现零偏压峰(ZBP)的证据,正如在拓扑超导体(16-19)的MQP态存在时所预期的那样。然而,在这类装置中检测到的ZBP也可能是由近藤效应或无序引起的。纳米线研究的一个关键缺点是它们缺乏空间分辨ZBP特征的能力,以便证明它们定位在带隙超导相的边界上。
Nadj-Perge等人介绍了一种制备一维(1D)拓扑超导体并检测其多量子点(MQP)的方法,该方法可以同时达到空间分辨率和光谱分辨率。已提出在传统s波超导体表面建立磁性原子链,以提供实现拓扑超导体的通用平台。
该平台可用于扫描隧道显微镜(STM)对多量子点的检测。在没有本征自旋-轨道耦合的情况下,以前的理论工作已经表明,当原子链中的磁性原子具有空间调制的自旋排列(例如,自旋螺旋)时,原子链中会出现拓扑相。链的自旋织构模拟了创建拓扑相所需的自旋轨道和塞曼相互作用的组合。 然而,在原子链中,螺旋自旋构型比简单的铁磁和反铁磁构型要少得多,或者可能更受无序的影响(31)。因此,我们通过在Pb表面放置一条铁链来探索另一种更容易实现的方案(图1A)。 我们将证明在这种情况下拓扑超导的基本成分是在Fe-Fe键距实现的Fe原子之间的铁磁相互作用和超导Pb(32)中强的自旋-轨道相互作用。 我们的方法与早先提出的利用半金属铁磁体或金属链在存在自旋轨道相互作用的情况下与超导体接触的拓扑超导电性有关。
4. 表面 TI 薄膜
shiba bound state
: placing magnetic chain on \(s\)-wave SC , the magnetic impurities form a spin helix due to RKKY and induce shiba BS
semianalytical tools to determine topo character of shiba chain
本征
Cu\(_x\)Bi\(_2\)Se\(_3\)掺杂
铁基
前面提到复合体系中常选择常规超导,但如果在高温超导中实现本征的拓扑超导,将在更高的温度鲁棒地研究马约拉纳费米子相关的物理。但自旋单重态的限制使得铁基超导体很难处于本征的拓扑超导态。但是在铁基超导体中,存在其他途径可以实现拓扑超导态。
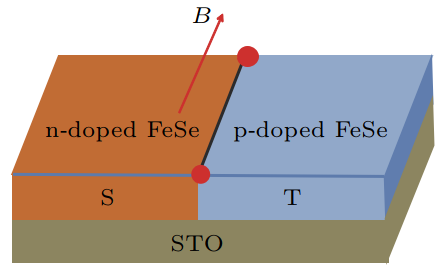
图 5 给出了一个分别由空穴掺杂和电子掺杂 的单层 FeSe/SrTiO\(_3\)构成的 p-n 结、空穴掺杂的部 分提供拓扑的边界态, 电子掺杂的部分提供超导 态, 两部分的边界在外加磁场或者铁磁绝缘体的作 用下可以形成一维的拓扑超导态。 在这种设计中, 拓扑和超导复合在同一种材料中, 因此可以通过改 变掺杂或者用不同的衬底来调制这种复合进而实 现拓扑超导。
Sr\(_2\)RuO\(_4\)
1994 年,Maeno 等人首先在 Sr\(_2\)RuO\(_4\)晶体中发现了超导电性,超导 \(T_c\)是 0.8 K(晶体质量提高后有所增加), 具有和高温超导类似的晶体结构。通过理论计算发现,它具有破坏时间反演对称性的自旋为三重态的 \(p_x\pm ip_y\)配对方式。在之后的核磁共振、磁光Kerr效应、中子散射、输运测量等实验中得到验证
kagome晶格
PRX11, 031026 (2021) X.H.Chen.
在具有SC基态的\(\mathbb{Z}_2\)拓扑Kagome金属CsV\(_3\)Sb\(_5\)中的发现涡旋核中的ZBCP,在远离Cs表面涡旋中心的地方分裂出来。这一现象让人联想到Bi\(_2\)Te\(_3\)/NbSe\(_2\)中曾经观察到的。最后," Our findings may have provided the first glimpse into possible Majorana modes in a kagome superconductor."
2M-WS\(_2\)
2019年,Fang Yuqiang et al. 通过\(1T\)-WS\(_2\)合成了2\(M\)-WS\(_2\)。经过测试,具有\(T_c=8.8\)K的超导转变温度,这是未经调制的TMD类材料中最高的。通过Shubnikov-de Haas震荡和第一性原理计算发现其电子结构具有很强的各向异性。此外,第一性原理计算还预测其具有\(Z_2\)拓扑不变量保护的单Dirac 锥。
Li Y.W. et al. 通过同步辐射和ARPES,观察到了拓扑表面态。
非中心对称超导体(non-centrosymmetric superconductor,NCS)
Intro
2004年,Bauer等人发现了第一个非中心对称超导体CePt\(_3\)Si,随后UIr、Li\(_2\)Pd\(_3\)B、CeRhSi\(_3\)、LaPtBi、PbTaSe\(_2\)等非中心对称超导体被发现。因为其没有空间反演对称性的特点,导致出现一些特别的物理性质,对于研究超导、拓扑物态都有很大的意义。
对于cooper pairs来说,配对形成依赖与时间反演和反转对称性。对spin-singlet配对缺失TRS会抑制,对spin-triplet,inversion symmetric则是必须的。由于金属性材料对电场的屏蔽效果,不便于直接改变反转对称性。但如果晶体本身不具有反转中心,那就会使得研究更容易进行。
考虑两种对称性操作,空间反演对称性P和时间反演对称性T,对于一个动量空间波矢k,存在两个单粒子简并态,\(\ket{k,a}\)和\(TP\ket{k,a}\)。当空间反演对称性被移除后,存在的相互作用使这两种态简并劈裂,也就是反对称自旋轨道耦合(Anti-symmetric spin-orbit coupling),这可以诱导一些奇特的物理性质。例如在二维电子气中,在准粒子激发中加入Rashba SOC 后,会产生一个能量为\(\epsilon_\pm=\frac{\hbar k^2}{2m}\pm \alpha|k|\)的螺旋态(helicity state),如图6
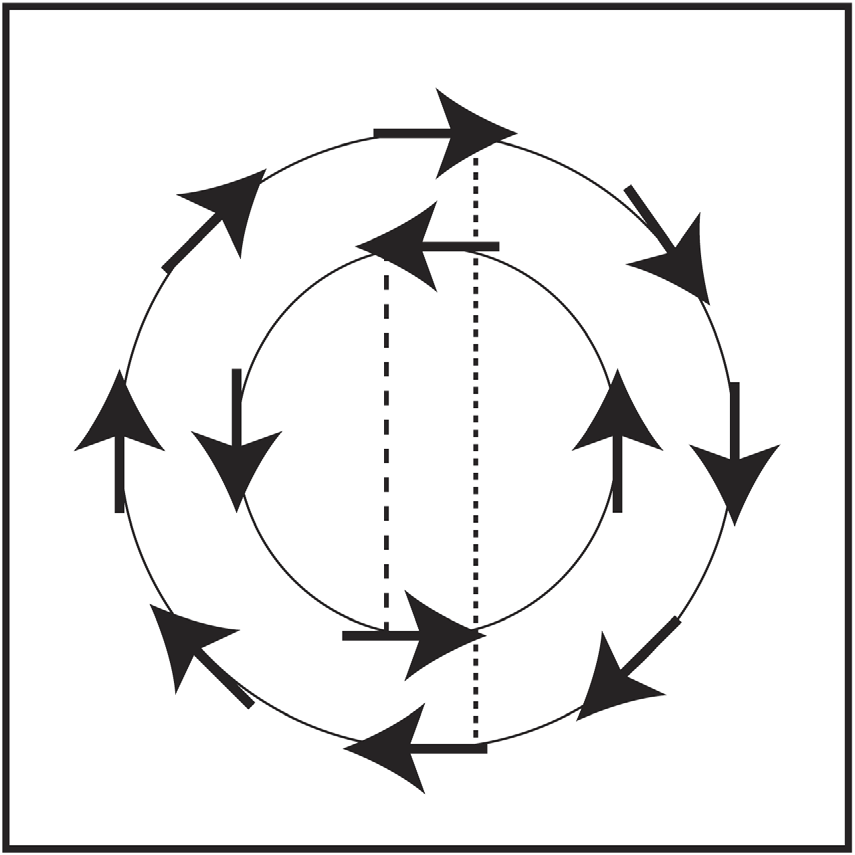
对于Rashba自旋轨道耦合效应比超导能隙更大的情况,从图6中可以看出,每一个方向只能在费米面上存在两个零动量的库珀对并且在图中用虚线标出。所有库珀对来自于自旋方向相反的一对电子,这表明将不存在自旋相同的库珀对。换而言之,在这种情况下不存在\(\ket{k,\uparrow}\) \(/\ket{k,\uparrow}\)或者\(\ket{k,\downarrow}\)/\(\ket{k,\downarrow}\)的库珀对。这种特性虽然是在Rashba自旋轨道耦合情况下考虑,事实上在所有缺失空间反演对称性的反对称自旋轨道耦合情况下都存在这种情况。对于存在空间反演对称性的系统,是可能存在一个自旋单态和三个自旋三重态。正如上面讨论的,如果移除了空间反演对称性,反对称自旋轨道耦合将会抑制三个自旋三重态中两个的超导转变温度,一旦反对称自旋轨道耦合能量大于超导能隙,只有一个自旋三重态能够保留下来。
总的来说自旋单态不会受到空间反演对称性的影响,并且有一个单一的自旋三重态会受到保护。
进一步考虑超导态,处在螺旋态的自选单态可表示为\[\ket{\psi_s}=\dfrac{(\ket{k,\uparrow}\ket{-k,\downarrow}+\ket{k,\downarrow}\ket{-k,\uparrow})}{\sqrt{2}}\] 如果反对称自旋轨道耦合足够大的话,那么各个螺旋态之间的配对可以忽略,我们可以得到: \[\label{helicsinglet} \ket{\psi_s}=\frac{i}{2\sqrt{2}} (-e^{i\phi_k}\ket{k,+0}\ket{-k,+}+e^{i\phi_k}\ket{k,-}\ket{-k,-})\]
考虑动量沿着y方向的情况,上述方程中的两个库珀对将会符合图6。方程[helicsinglet]表明了自旋单态的超导体在每个螺旋态上有着相同的能隙大小。通常情况下没有理由对于各个螺旋态具有相同的能隙大小,事实上,不同的能隙是可以存在的,这表明了自旋单态和自旋三重态的共存,这种混合形式在空间对称性缺失的情况下可以实现。
值得注意的是,由泡利不相容原理表明自旋三重态为奇宇称而自旋单态则为偶宇称,显然,当存在空间反演对称性时,这种混合将不能存在。所以这种自旋单态和自旋三重态的混合模式是非中心对称超导体所特有的性质。
在对NCS材料的研究中,ASOC允许自旋单态、三态的混合情况出现,是 一个重要的效应。在弱电子关联的材料中,ASOC的影响是比较容易区分出来的。例如在Li\(_2\)Pd\(_3\)B和Li\(_2\)Pt\(_3\)B中已经得到实验验证。 在众多NCS材料中,有一些被认为是拓扑超导的候选材料,例如YPtBi,BiPd和PbTaSe\(_2\)
对众多的NCS材料,可以分成NCS重费米子超导材料、弱关联的节超导材料、完全带隙弱关联的超导等类型。
NCS重费米子超导材料
CePt\(_3\)Si
CePt\(_3\)Si是第一个被报道的非中心对称重费米子超导体,也是唯一一个被证实在常压下表现出超导电性的。非中心对称的四方晶体结构(空间群\(P4 mm\)),其中缺少垂直于c轴的镜面消除了反转对称性,导致Rashba型ASOC。当时\(T_{\rm N}\) = 2.2 K,系统按反铁磁性排列,其中磁矩位于ab平面内,在平面内铁磁排列,但在相邻层之间反铁磁排列。其中的反铁磁性与超导电性之间的关系尤其令人感兴趣。\(\mu\)子自旋弛豫(\(\mu\)SR)测量表明,所有的\(\mu\)子都被注入到样品的磁有序区域,因此,磁性相和超导相之间存在微观共存,而不是在其他一些重费米子超导体(如CeCu\(_2\)Si\(_2\))中观察到的相之间的竞争。
它还被认为是非常规超导体,一是其超导态对非磁性杂质很敏感,4%的Th替代Ce或10%-15%的Ge替代硅就可以抑制超导电性。CePt\(_3\)Si\(_0.94\)Ge\(_0.06\)的压力研究表明,\(T_c\)的抑制不能用Ge替代的负化学压力来解释,而是由于非磁性杂质对非常规超导电性的配对断开效应所致。电子对比热的贡献除以温度\(C_{el}/T\),在很大的温度范围内(高达0.3 K左右)呈现线性行为,这是线节存在的证,而不是完全带隙超导体的指数行为。
CeTX\(_3\) (T = transition metal, X = Si or Ge).
除了CePt\(_3\)Si在常压下的超导电性外,在CeTX\(_3\)(T=过渡金属,=X Si,Ge)系列中的几个化合物中还发现了压力诱导超导电性,它们以图4(B)插图所示的体心四方晶体结构(空间群\(I4 mm\))结晶。 与CePt\(_3\)Si的晶体结构非常相似,没有垂直于c轴的镜面,这导致了反转对称性的破坏。据报道,其中四种化合物显示出超导性, CeRhSi\(_3\) for \(p~>\) 1.2 GPa , CeIrSi\(_3\) for \(p~>\) 1.8 GPa , CeCoGe\(_3\) for \(p~>\) 4.3 GPa and CeIrGe\(_3\) for \(p~>\) 20 GPa 。所有这些化合物在常压下都是反铁磁性有序的,但施加压力会抑制\(T_N\),从而观察到超导穹顶。CeTX\(_3\)的性质通常在Doniach相图[56,57]的上下文中解释,在该相图中,导致磁性有序的位间Ruderman-Kittel-Kasuya-Yosida(RKKY)相互作用和有利于形成非磁性单态的在位Kondo相互作用之间存在竞争.
CeTX\(_3\)超导体的一个显著特征是\(H_{C2}(T)\)的极大和各向异性的值[69-71],如图 [fig5]对于施加在ab平面上的场,CeRhSi\(_3\)的\(H_{c2}(0)\)达到约\(7\) T,但是对于沿c轴施加的场,\(H_{c2}(0)\)要大得多,其中\(H_{c2}(T)\)显示出在p=2.9 GPa时在T=0时达到 30 T的向上曲率。如插图所示,沿着c轴的行为明显偏离了通常用于描述传统BCS超导体的Werthamer-Helfand-Hohenberg(WHH)模型。这些值表明,与CePt\(_3\)Si的情况一样,BCS Pauli限制场在所有方向上都被超过,但与在\(H_{C2}(T)\)中仅表现出小的各向异性的CePt\(_3\)Si不同,CeTX\(_3\)中沿c轴施加的场的值要大得多。

这与这种结构的受保护三重态的自旋磁化率的计算是一致的,这些计算表明在一个方向上没有泡利限制,而在其他方向上有一个增强的泡利限制场。在这种情况下,\(H_{C2}(T)\)将受到\(H_{\parallel ab}\)的顺磁对破裂的限制,但仅由\(H_{\parallel c}\)的轨道限制场决定,该限制场可能在QCP附近增强[72,73]。在这种情况下,预测在涡旋状态下磁化强度垂直于外加磁场\(H_{\parallel ab}\)。
为了进一步表征配对状态,还对CeIrSi\(_3\)进行了NMR测量([Figs. 7(b) and (c)])。多晶样品的核磁共振测量表明,\(T^3\) 依赖于\(1/T_1\),在\(T_c\)以下没有相干峰,这表明在超导带隙中有线节点的非传统配对态(图5(B))[74],类似于其他几个重费米子超导体。这些测量是在 \(2.7~-~2.8\) GPa的压力下进行的,此时反铁磁性被完全抑制,在正常状态下,\(1/T_1\)表现出\(\sim T/\sqrt{T+\theta}\) 依赖关系,\(\theta\sim0\)在2.7 GPa,这表明它非常接近QCP。还在2.8 GPa的压力下对单晶进行了NMR测量,如图 7(c)所示,虽然沿[001]方向施加的磁场在Tc以下的奈特位移没有变化,但沿[110]方向的磁场有明显的下降,这与在CePt\(_3\)Si中观察到的各向同性常数值明显不同。 这种\(H\perp c\) 奈特偏移的减小更符合在强自旋-轨道耦合极限下的预期行为。然而,奈特偏移的降幅仍然相对较小,仅达到正常状态值的90%,而预期的降幅为50%,这可能再次表明由于强电子关联而有所增强。
弱关联的节超导体体系
参考文献
Stevan Nadj-Perge, Ilya K. Drozdov, Jian Li, Hua Chen, Sangjun Jeon, Jungpil Seo, Allan H. MacDonald, B. Andrei Bernevig, and Ali Yazdani. Observation of majorana fermions in ferromagnetic atomic chains on a superconductor. , 346(6209):602–607, 2014.
Satoshi Sasaki, M. Kriener, Kouji Segawa, Keiji Yada, Yukio Tanaka, Masatoshi Sato, and Yoichi Ando. Topological superconductivity in \({\mathrm{cu}}_{x}{\mathrm{bi}}_{2}{\mathrm{se}}_{3}\). , 107:217001, Nov 2011.
Yi Zhang, Kun Jiang, Fuchun Zhang, Jian Wang, and Ziqiang Wang. 铁基超导中拓扑量子态研究进展. , 67:207101, 2019.
Dongfei Wang, Lingyuan Kong, Peng Fan, Hui Chen, Shiyu Zhu, Wenyao Liu, Lu Cao, Yujie Sun, Shixuan Du, John Schneeloch, Ruidan Zhong, Genda Gu, Liang Fu, Hong Ding, and Hong-Jun Gao. Evidence for majorana bound states in an iron-based superconductor. , 362(6412):333–335, 2018.
Peng Zhang, Koichiro Yaji, Takahiro Hashimoto, Yuichi Ota, Takeshi Kondo, Kozo Okazaki, Zhijun Wang, Jinsheng Wen, G. D. Gu, Hong Ding, and Shik Shin. Observation of topological superconductivity on the surface of an iron-based superconductor. , 360(6385):182–186, 2018.
Jing Xia, Yoshiteru Maeno, Peter T. Beyersdorf, M. M. Fejer, and Aharon Kapitulnik. High resolution polar kerr effect measurements of \({\mathrm{sr}}_{2}{\mathrm{ruo}}_{4}\): Evidence for broken time-reversal symmetry in the superconducting state. , 97:167002, Oct 2006.
Yuji Ueno, Ai Yamakage, Yukio Tanaka, and Masatoshi Sato. Symmetry-protected majorana fermions in topological crystalline superconductors: Theory and application to \({\mathrm{sr}}_{2}{\mathrm{ruo}}_{4}\). , 111:087002, Aug 2013.
Hengxin Tan, Yizhou Liu, Ziqiang Wang, and Binghai Yan. Charge density waves and electronic properties of superconducting kagome metals. , 127:046401, Jul 2021.
Zuowei Liang, Xingyuan Hou, Fan Zhang, Wanru Ma, Ping Wu, Zongyuan Zhang, Fanghang Yu, J.-J. Ying, Kun Jiang, Lei Shan, Zhenyu Wang, and X.-H. Chen. Three-dimensional charge density wave and surface-dependent vortex-core states in a kagome superconductor \({\mathrm{csv}}_{3}{\mathrm{sb}}_{5}\). , 11:031026, Aug 2021.
Zheng H.J. Fang Y.Q. Li, Y.W. Observation of topological superconductivity in a stoichiometric transition metal dichalcogenide 2m-ws2. , 12:2874, 2021.
Yuqiang Fang, Jie Pan, Dongqin Zhang, Dong Wang, Hishiro T. Hirose, Taichi Terashima, Shinya Uji, Yonghao Yuan, Wei Li, Zhen Tian, Jiamin Xue, Yonghui Ma, Wei Zhao, Qikun Xue, Gang Mu, Haijun Zhang, and Fuqiang Huang. Discovery of superconductivity in 2m ws2 with possible topological surface states. , 31(30):1901942, 2019.
Pan J. Wang X. et al. Yuan, Y. Evidence of anisotropic majorana bound states in 2m-ws2. , 15:1046, 2019.
E. Bauer, G. Hilscher, H. Michor, Ch. Paul, E. W. Scheidt, A. Gribanov, Yu. Seropegin, H. Noël, M. Sigrist, and P. Rogl. Heavy fermion superconductivity and magnetic order in noncentrosymmetric \({\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}}_{3}\mathrm{S}\mathrm{i}\). , 92:027003, Jan 2004.
M Smidman, M B Salamon, H Q Yuan, and D F Agterberg. Superconductivity and spinorbit coupling in non-centrosymmetric materials: a review. , 80(3):036501, jan 2017.
Ichirô Satake. The gauss-bonnet theorem for v-manifolds. , 9:464–492., 1957.
Di Xiao, Ming-Che Chang, and Qian Niu. Berry phase effects on electronic properties. , 82:1959–2007, Jul 2010.
Shinsei Ryu, Andreas P Schnyder, Akira Furusaki, and Andreas W W Ludwig. Topological insulators and superconductors: tenfold way and dimensional hierarchy. , 12(6):065010, jun 2010.
Ching-Kai Chiu, Hong Yao, and Shinsei Ryu. Classification of topological insulators and superconductors in the presence of reflection symmetry. , 88:075142, Aug 2013.
Rui Yu, Xiao Liang Qi, Andrei Bernevig, Zhong Fang, and Xi Dai. Equivalent expression of \({\mathbb{z}}_{2}\) topological invariant for band insulators using the non-abelian berry connection. , 84:075119, Aug 2011.
https://zhuanlan.zhihu.com/p/25432728.
Yi Zhang, Kun Jiang, Fuchun Zhang, Jian Wang, and Ziqiang Wang. Atomic line defects and topological superconductivity in unconventional superconductors. , 11:011041, Mar 2021.
P. Krogstrup C. M. Marcus S. Vaitiekenas, Y. Liu. Zero-bias peaks at zero magnetic field in ferromagnetic hybrid nanowires. , 17:43–47, 2021.
Chun-Xiao Liu, Sergej Schuwalow, Yu Liu, Kostas Vilkelis, A. L. R. Manesco, P. Krogstrup, and Michael Wimmer. Electronic properties of inas/eus/al hybrid nanowires. , 104:014516, Jul 2021.
Yu Liu, Saulius Vaitiekėnas, Sara Martí-Sánchez, Christian Koch, Sean Hart, Zheng Cui, Thomas Kanne, Sabbir A. Khan, Rawa Tanta, Shivendra Upadhyay, Martin Espiñeira Cachaza, Charles M. Marcus, Jordi Arbiol, Kathryn A. Moler, and Peter Krogstrup. Semiconductor–ferromagnetic insulator–superconductor nanowires: Stray field and exchange field. , 20(1):456–462, 2020. PMID: 31769993.
Samuel D. Escribano, Elsa Prada, Yuval Oreg, and Alfredo Levy Yeyati. Tunable proximity effects and topological superconductivity in ferromagnetic hybrid nanowires. , 104:L041404, Jul 2021.
S. Nadj-Perge, I. K. Drozdov, B. A. Bernevig, and Ali Yazdani. Proposal for realizing majorana fermions in chains of magnetic atoms on a superconductor. , 88:020407, Jul 2013.
Falko Pientka, Leonid I. Glazman, and Felix von Oppen. Unconventional topological phase transitions in helical shiba chains. , 89:180505, May 2014.
Joel Röntynen and Teemu Ojanen. Topological superconductivity and high chern numbers in 2d ferromagnetic shiba lattices. , 114:236803, Jun 2015.
Nicholas Sedlmayr, Vardan Kaladzhyan, and Cristina Bena. Analytical and semianalytical tools to determine the topological character of shiba chains. , 104:024508, Jul 2021.
Manfred Sigrist, D.F. Agterberg, P.A. Frigeri, N. Hayashi, R.P. Kaur, A. Koga, I. Milat, K. Wakabayashi, and Y. Yanase. Superconductivity in non-centrosymmetric materials. , 310(2, Part 1):536–540, 2007. Proceedings of the 17th International Conference on Magnetism.
P. A. Frigeri, D. F. Agterberg, A. Koga, and M. Sigrist. Superconductivity without inversion symmetry: Mnsi versus \({\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}}_{3}\mathrm{S}\mathrm{i}\). , 92:097001, Mar 2004.
H. Q. Yuan, D. F. Agterberg, N. Hayashi, P. Badica, D. Vandervelde, K. Togano, M. Sigrist, and M. B. Salamon. \(s\)-wave spin-triplet order in superconductors without inversion symmetry: \({\mathrm{li}}_{2}{\mathrm{pd}}_{3}\mathrm{B}\) and \({\mathrm{li}}_{2}{\mathrm{pt}}_{3}\mathrm{B}\). , 97:017006, Jul 2006.
M. Nishiyama, Y. Inada, and Guo-qing Zheng. Spin triplet superconducting state due to broken inversion symmetry in \({\mathrm{li}}_{2}{\mathrm{pt}}_{3}\mathrm{B}\). , 98:047002, Jan 2007.
Hyunsoo Kim, Kefeng Wang, Yasuyuki Nakajima, Rongwei Hu, Steven Ziemak, Paul Syers, Limin Wang, Halyna Hodovanets, Jonathan D. Denlinger, Philip M.R. Brydon, Daniel F. Agterberg, Makariy A. Tanatar, Ruslan Prozorov, and Johnpierre Paglione. . , 4(4):1–7, 2018.
Enayat M. Maldonado A. et al. Sun, Z. Dirac surface states and nature of superconductivity in noncentrosymmetric bipd. , 6:6633, 2015.
Mazhar N. Ali, Quinn D. Gibson, T. Klimczuk, and R. J. Cava. Noncentrosymmetric superconductor with a bulk three-dimensional dirac cone gapped by strong spin-orbit coupling. , 89:020505, Jan 2014.
N. Kimura, K. Ito, K. Saitoh, Y. Umeda, H. Aoki, and T. Terashima. Pressure-induced superconductivity in noncentrosymmetric heavy-fermion \({\mathrm{cerhsi}}_{3}\). , 95:247004, Dec 2005.
Ichiro Sugitani, Yusuke Okuda, Hiroaki Shishido, Tsutomu Yamada, Arumugam Thamizhavel, Etsuji Yamamoto, Tatsuma D. Matsuda, Yoshinori Haga, Tetsuya Takeuchi, Rikio Settai, and Yoshichika Ōnuki. Pressure-induced heavy-fermion superconductivity in antiferromagnet ceirsi3 without inversion symmetry. , 75(4):043703, 2006.
R. Settai, I. Sugitani, Y. Okuda, A. Thamizhavel, M. Nakashima, Y. Ōnuki, and H. Harima. Pressure-induced superconductivity in cecoge3 without inversion symmetry. , 310(2, Part 1):844–846, 2007. Proceedings of the 17th International Conference on Magnetism.
Fuminori Honda, Ismardo Bonalde, Shingo Yoshiuchi, Yusuke Hirose, Taichi Nakamura, Katsuya Shimizu, Rikio Settai, and Yoshichika Ōnuki. Pressure-induced superconductivity in non-centrosymmetric compound ceirge3. , 470:S543–S544, 2010. Proceedings of the 9th International Conference on Materials and Mechanisms of Superconductivity.
Philip W. Anderson. . CRC Press, 1994.
Xun Shi, Zhi-Qing Han, Pierre Richard, Xian-Xin Wu, Xi-Liang Peng, Tian Qian, Shan-Cai Wang, Jiang-Ping Hu, Yu-Jie Sun, and Hong Ding. Fete1−xsex monolayer films: towards the realization of high-temperature connate topological superconductivity. , 62(7):503–507, 2017.
Lev P. Gor’kov and Emmanuel I. Rashba. Superconducting 2d system with lifted spin degeneracy: Mixed singlet-triplet state. , 87:037004, Jul 2001.
N. P. Butch, P. Syers, K. Kirshenbaum, A. P. Hope, and J. Paglione. Superconductivity in the topological semimetal yptbi. , 84:220504, Dec 2011.
Wensen Wei, G. J. Zhao, D. R. Kim, Chiming Jin, J. L. Zhang, Langsheng Ling, Lei Zhang, Haifeng Du, T. Y. Chen, Jiadong Zang, Mingliang Tian, C. L. Chien, and Yuheng Zhang. \(\mathrm{R}{\mathrm{h}}_{2}\mathrm{M}{\mathrm{o}}_{3}\mathrm{N}\): Noncentrosymmetric \(s\)-wave superconductor. , 94:104503, Sep 2016.
Wei Li, Chiming Jin, Renchao Che, Wensen Wei, Langsheng Lin, Lei Zhang, Haifeng Du, Mingliang Tian, and Jiadong Zang. Emergence of skyrmions from rich parent phases in the molybdenum nitrides. , 93:060409, Feb 2016.
Zhang P. Shen B. et al Xie, W. Captas: A new noncentrosymmetric superconductor. , 63:237412, 2020.
T. Shang, M. Smidman, A. Wang, L.-J. Chang, C. Baines, M. K. Lee, Z. Y. Nie, G. M. Pang, W. Xie, W. B. Jiang, M. Shi, M. Medarde, T. Shiroka, and H. Q. Yuan. Simultaneous nodal superconductivity and time-reversal symmetry breaking in the noncentrosymmetric superconductor captas. , 124:207001, May 2020.
Syu-You Guan, Peng-Jen Chen, and Tien-Ming Chuang. Topological surface states and superconductivity in non-centrosymmetric PbTaSe2. , 60(SE):SE0803, may 2021.