转载地址:WannierTools教程之拓扑绝缘体---Bi2Se3 - WannierTools - 材料基因论坛 MaterialsGene
作者: Brook
首发日期:2017.02.21
********转载请保留********
以后WannierTools官方的中文教程将会在材料基因论坛发布,欢迎大家参与讨论。在所有教程完成之前,请大家阅读www.wanniertools.com上的说明文档。
本系列教程将以多个例子的形式来开展,其中包括拓扑绝缘体,Weyl半金属,Dirac半金属,Triple point金属,Nodal
line半金属等等。每当出现一种新的拓扑体系,我们都将尝试用WannierTools去重复前人的结果,尽可能让WannierTools适用于所有
拓扑体系。
在首个教程中,我们以经典的Bi2Se3三维强拓扑绝缘体体系为例子,来展示如何从第一性原理模拟到构造Wannier函数,最后到利用WannierTools研究拓扑性质的全过程。
WannierTools
是一个基于紧束缚模型的程序包。这个紧束缚模型可以由人工构造,也可以有软件产生。但是格式是固定的,目前采用的格式是由Wannier90程序包所定义
(请参考Wannier90_hr.dat里的具体格式,后面会陆续完善所有涉及到的细节)。在此我们只介绍如何使用Wannier90程序和VASP构
造基于Wannier函数的紧束缚模型wannier90_hr.dat。
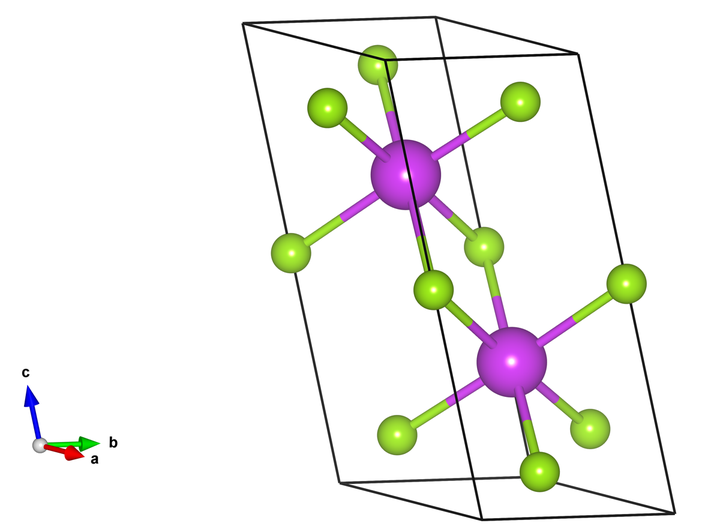
首先我们进行第一性原理模拟,软件选用VASP。由于我们知道Bi2Se3材料的解理面是垂直于c轴的面,因此我们在原包构造的时候就有意将(001)面设置为垂直c轴的面。这样有助于我们后面的表面态分析。选好的原胞POSCAR为:
Bi2Se3
1.0
-2.069 -3.583614 0.000000
2.069 -3.583614 0.000000
0.000 2.389075 9.546667
Bi Se
2 3
Direct
0.3990 0.3990 0.6970
0.6010 0.6010 0.3030
0 0 0.5
0.2060 0.2060 0.1180
0.7940 0.7940 0.8820
对于的结构示意图如下
画一下能带结构,然后再做一下Fatband分析,了解费米面附近能带是有哪些成分构成的。对于Bi2Se3,费米面附近的能带是有Bi原子和Se原子的px,py,pz轨道构成。于是构造Wannier函数的时候,可以选择这些轨道作为初始投影轨道。
接下来是构造Wannier函数。
有不少朋友反映VASP+Wannier90
v1.2在构造含有自旋轨道耦合体系中会失效。目前我没有碰到类似的问题,从我阅读VASP5.3—VASP5.4.1源码的经验来
看,Wannier90 v1.2完全可以和VASP+SOC兼容。 然而官网明确表示VASP和Wannier90
v2.0不兼容。Wannier90
v2.0确实增加了不少功能,不过就构造紧束缚模型这一点来说(也就是生成Wannier90_hr.dat),v2.0和v1.2并没有什么区别。
构造Wannier函数的时候,需要在INCAR中加入LWANNIER90 =
.TRUE.,另外提供一个wannier90.win文件。适用于Bi2Se3的wannier90.win文件为
num_wann = 30
num_bands = 60
dis_num_iter=1000
num_iter=0
iprint=2
!min of outer window
dis_win_min = -2.0
dis_win_max = 18.0
!inner -
dis_froz_min = -2.0000
dis_froz_max = 5.5000
hr_plot =.true.
begin projections
Bi : px; py; pz
Se : px; py; pz
end projections
spinors = .true.
这里需要注意的一点是,num_bands必须和你OUTCAR中的NBANDS一致。在并行运行VASP的时候,VASP会根据系统cpu个数和你指定的NBANDS个数来调整真实运行的NBANDS个数,因此需要特别注意一下。
小结:用VASP+wannier90构造Wannier函数的过程
- VASP做一个SCF计算,得到收敛的电荷密度。
- (选做) 做一个VASP能带计算,主要用来分析能带成分,以选择projectors和能带窗口用来构造Wannier函数。这个不是必须的,如果你已经知道了projectors和能带窗口的话,就不做了。
- 准备好wannier90.win文件,同时在INCAR里头添加一行LWANNIER90=.TRUE.和一行ICHARG=11,然后再运行一遍VASP。 顺利的话,会产生wannier90.amn, wannier90.mmn, wannier90.eig, wannier90.chk 等4个文件。wannier90.win里头的内容也有可能会被改变。请注意wannier90.win里头的num_bands要和OUTCAR里头的NBANDS一致。
- 运行wannier90主程序。wannier90.x wannier90 &
构造好Wannier函数以后,仔细检查一下wannier90.wout,
搜索”Final
State”,在这里可以看到每条Wannier轨道的展宽,由此可以检查你构造的Wannier函数是否足够局域。如果有某个Wannier函数的展宽
比晶格常数大许多,就表明你的Wannier函数构造不是很理想,需要不断调节投影轨道,解纠缠窗口以及Frozen窗口等。从这些轨道的中心和展宽也能
看出轨道之间的简并性如何,由此也可以判断所构造的Wannier函数对称性如何,这个也会影响后续的分析,特别是表面态的计算。
紧接着,你就可以开始书写WannierTools的主输入文件了,
目前叫input.dat,以后会改成http://wt.in (WannierTools v2.2之后)。 这里不具体介绍每一个参数,在说明文档中有详细的介绍,中文版的说明文档正在翻译中。
input.dat文件有模板,使用的时候直接拷贝然后加以修改。很多内容都可以直接从wannier90.win和wannier90.wout中拷
贝。 Bi2Se3的主输入文件input.dat可以在附件中下载得到。我们可以通过控制输入文件中的一些参数来实现我们所需要的功能。
1. 计算体能带,对比VASP计算的能带和Wannier TB得到的能带。输入文件中需要编辑的地方为,
&TB_FILE
Hrfile = 'wannier90_hr.dat'
Particle= 'electron'
/
LATTICE
Angstrom
-2.069 -3.583614 0.000000 ! crystal lattice information
2.069 -3.583614 0.000000
0.000 2.389075 9.546667
ATOM_POSITIONS
5 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
Bi 0.3990 0.3990 0.6970
Bi 0.6010 0.6010 0.3030
Se 0 0 0.5
Se 0.2060 0.2060 0.1180
Se 0.7940 0.7940 0.8820
PROJECTORS
3 3 3 3 3 ! number of projectors
Bi px py pz ! projectors
Bi px py pz
Se px py pz
Se px py pz
Se px py pz
&CONTROL
BulkBand_calc = T
/
&SYSTEM
SOC = 1 ! soc
E_FERMI = 4.4195 ! e-fermi
/
&PARAMETERS
Nk1 = 41 ! number k points odd number would be better
/
KPATH_BULK ! k point path
4 ! number of k line only for bulk band
G 0.00000 0.00000 0.0000 Z 0.00000 0.00000 0.5000
Z 0.00000 0.00000 0.5000 F 0.50000 0.50000 0.0000
F 0.50000 0.50000 0.0000 G 0.00000 0.00000 0.0000
G 0.00000 0.00000 0.0000 L 0.50000 0.00000 0.0000
直接运行wann_tools &
这里需要提到的是如果你不想运行其它功能,请在CONTROL中把其它所有的Flag都设成F,或者删除,只留下
&CONTROLBulkBand_calc = T
/
运
行完成后,可以在当前文件夹下看到bulkek.gnu, bulkek.dat.
使用gnuplot5.0以上版本的软件,就可以得到bulkek.eps图。 命令为gnuplot bulkek.gnu 。
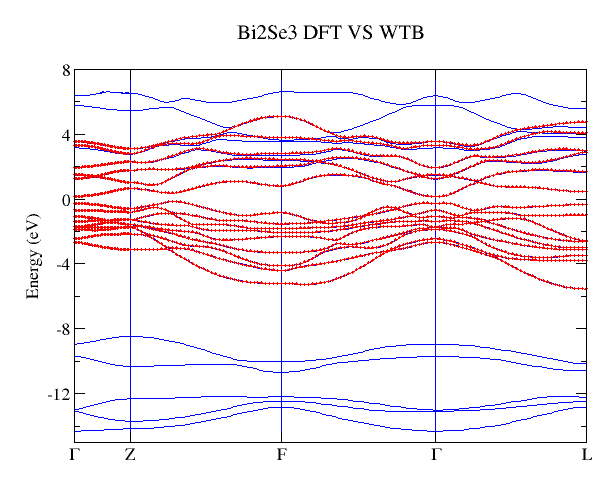
下图是VASP计算的能带(蓝色)和Wannier
TB得到的能带(红色)对比图,从图中可以看出我们构造的Wannier函数能够很好在费米面附近重复第一性原理的得到的能带。
2. 计算Z2数,最新的版本可以直接计算三维绝缘体的拓扑数。
输入文件为
&TB_FILE
Hrfile = 'wannier90_hr.dat'
Particle= 'electron'
/
LATTICE
Angstrom
-2.069 -3.583614 0.000000 ! crystal lattice information
2.069 -3.583614 0.000000
0.000 2.389075 9.546667
ATOM_POSITIONS
5 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
Bi 0.3990 0.3990 0.6970
Bi 0.6010 0.6010 0.3030
Se 0 0 0.5
Se 0.2060 0.2060 0.1180
Se 0.7940 0.7940 0.8820
PROJECTORS
3 3 3 3 3 ! number of projectors
Bi px py pz ! projectors
Bi px py pz
Se px py pz
Se px py pz
Se px py pz
&CONTROL
Z2_3D_calc = T
/
&SYSTEM
SOC = 1 ! soc
NumOccupied = 18 ! Number of occupied Wannier bands
/
&PARAMETERS
Nk1 = 41 ! number k points odd number would be better
Nk2 = 41 ! number k points odd number would be better
/
运行wann_tools&完毕后,可以得到
wanniercenter3D_Z2.gnu, wanniercenter3D_Z2_1.dat wanniercenter3D_Z2_3.dat wanniercenter3D_Z2_5.dat
wanniercenter3D_Z2_2.dat wanniercenter3D_Z2_4.dat wanniercenter3D_Z2_6.dat 共7个文件,同样通过gnuplot wanniercenter3D_Z2.gnu命令可以得到wanniercenter3D_Z2.eps文件。 结果如下:
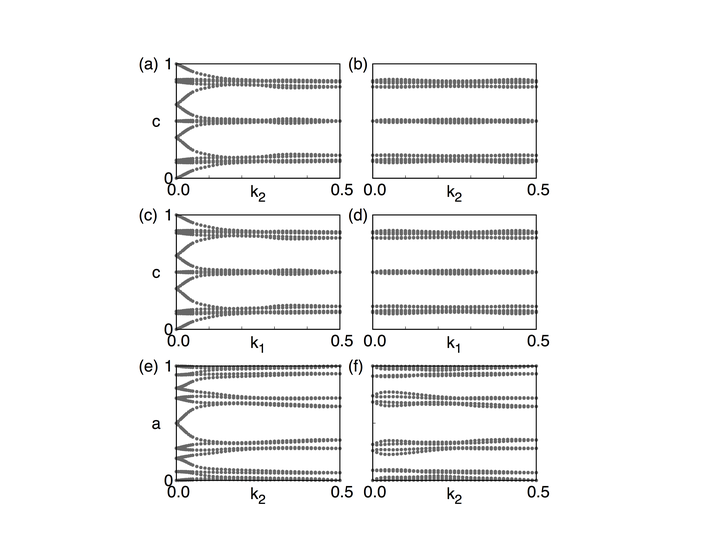
这
幅图画的是Wilson loop(Wannier Charge Center)随着k点的变化。具体的定义和物理含义大家可以参考Yu Rui
et.al(2011), Alexey A. Soluyanov et.al (2011) 两篇文献。
首先说明一个概念,我们通常所说的Z2数是在一个2维闭合曲面内定义的一个拓扑数,比如在kx=0的平面内(由于布里渊区的周期性,所以有闭合曲面的概
念)。这里a-f六幅图分别画的是在 k1=0.0、 k1=0.5、 k2=0.0、 k2=0.5、 k3=0.0、 k3=0.5平面内的Wilson loop演化图,从这些演化图中可以知道每一幅图的Z2数。规则是:在图中画一条从左到右的曲线,数这条曲线和图中曲线的交叉点个数,如果交叉点个数为奇数,那么Z2数为1,如果为偶数,那么Z2数为0。 这个交叉数并不会因为你画的曲线不同而不同。 知道了这6个数后,我们就可以通过Fu Liang 在2007年提出的方法(Phys. Rev. Lett. 98, 106803)
来
判断这个绝缘体的拓扑指数。 对于Bi2Se3,拓扑指数为(1;000),根据Fu的定义,我们知道Bi2Se3是强拓扑绝缘体。
这里可以多谈一点,我们计算过程中计算了6个Z2数,然而这六个数并不是各自独立的,他们满足一个等式
[tex]X_0+X_1=Y_0+Y_1=Z_0+Z_1[/tex].其中X、Y、Z分别对应上面的1、2、3.
有趣的是,如果你计算得到的这六个数并不满足这个等式的话,那么恭喜你,你找到了一个Dirac材料。因为Dirac点的出现会改变Z2数,从而破坏了等
式。
3. 计算表面态
表
面态是拓扑材料的一个重要的特征,也是理论与实验之间最直接的桥梁。理论中计算出来的表面态,可以直接与试验中的ARPES数据相比,从而间接的验证理论
的正确性。 在WannierTools中,我们可以计算任意界面的表面态,这点需要用户仔细阅读文档中关于SURFACE CARD这段。
这里我们只计算Bi2Se3解理面的表面态, 输入文件为:
&TB_FILE
Hrfile = 'wannier90_hr.dat'
Particle= 'electron'
/
LATTICE
Angstrom
-2.069 -3.583614 0.000000 ! crystal lattice information
2.069 -3.583614 0.000000
0.000 2.389075 9.546667
ATOM_POSITIONS
5 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
Bi 0.3990 0.3990 0.6970
Bi 0.6010 0.6010 0.3030
Se 0 0 0.5
Se 0.2060 0.2060 0.1180
Se 0.7940 0.7940 0.8820
PROJECTORS
3 3 3 3 3 ! number of projectors
Bi px py pz ! projectors
Bi px py pz
Se px py pz
Se px py pz
Se px py pz
&CONTROL
SlabSS_calc = T
SlabArc_calc = T
/
&SYSTEM
SOC = 1 ! soc
NumOccupied = 18 ! Number of occupied Wannier bands
E_FERMI = 4.4195 ! e-fermi
/
&PARAMETERS
Eta_Arc = 0.001 ! infinite small value, like brodening
E_arc = 0.0 ! energy for calculate Fermi Arc
OmegaMin = -0.6 ! energy interval
OmegaMax = 0.5 ! energy interval
OmegaNum = 401 ! omega number
Nk1 = 101 ! number k points odd number would be better
Nk2 = 101 ! number k points odd number would be better
/
SURFACE ! See doc for details
1 0 0
0 1 0
0 0 1
KPATH_SLAB
2 ! numker of k line for 2D case
K 0.33 0.67 G 0.0 0.0 ! k path for 2D case
G 0.0 0.0 M 0.5 0.5
KPLANE_SLAB
-0.1 -0.1 ! Original point for 2D k plane
0.2 0.0 ! The first vector to define 2D k plane
0.0 0.2 ! The second vector to define 2D k plane for arc plots
得到的结果为
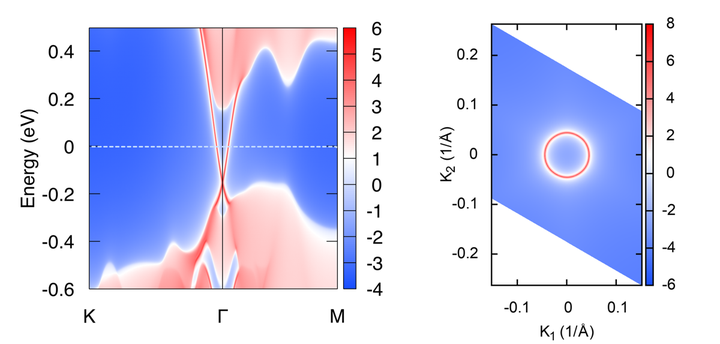
4. 计算表面态上的自旋分布
一般拓扑绝缘体都伴随着强SOC,表面态上的自旋和动量总是锁定在一起的,形成特殊的Spin-texture。 WannierTools满足了这一需求,输入文件中特殊指定的为
&TB_FILE
Hrfile = 'wannier90_hr.dat'
Particle= 'electron'
/
LATTICE
Angstrom
-2.069 -3.583614 0.000000 ! crystal lattice information
2.069 -3.583614 0.000000
0.000 2.389075 9.546667
ATOM_POSITIONS
5 ! number of atoms for projectors
Direct ! Direct or Cartisen coordinate
Bi 0.3990 0.3990 0.6970
Bi 0.6010 0.6010 0.3030
Se 0 0 0.5
Se 0.2060 0.2060 0.1180
Se 0.7940 0.7940 0.8820
PROJECTORS
3 3 3 3 3 ! number of projectors
Bi px py pz ! projectors
Bi px py pz
Se px py pz
Se px py pz
Se px py pz
&CONTROL
SlabSpintexture_calc = F
/
&SYSTEM
SOC = 1 ! soc
E_FERMI = 4.4195 ! e-fermi
/
&PARAMETERS
Eta_Arc = 0.001 ! infinite small value, like brodening
E_arc = 0.0 ! energy for calculate Fermi Arc
Nk1 = 101 ! number k points odd number would be better
Nk2 = 101 ! number k points odd number would be better
/
SURFACE ! See doc for details
1 0 0
0 1 0
0 0 1
KPLANE_SLAB
-0.1 -0.1 ! Original point for 2D k plane
0.2 0.0 ! The first vector to define 2D k plane
0.0 0.2 ! The second vector to define 2D k plane for arc plots
结果为
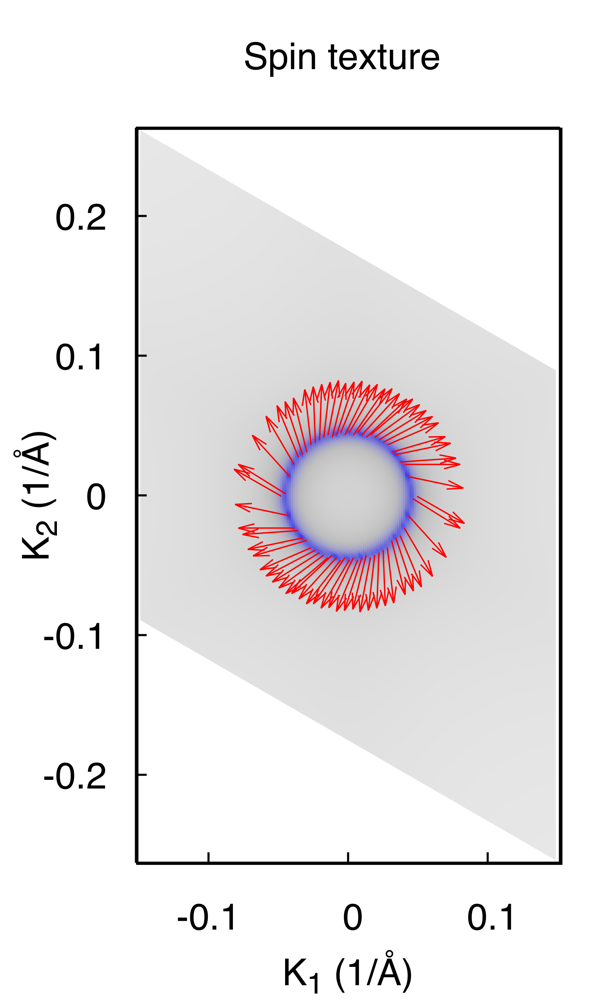
Note: 计算Spin texture时,我们假定你构造的经束缚模型的基矢自旋上和自旋下没有耦合在一起。 这个依赖于你构造的Wannier函数的质量。 如果对此计算不放心,可以结合第一性原理计算和Wannier90进行spintexture计算。
总结: Bi2Se3是一个标准的例子,每一个进入拓扑材料领域的人都必须要学习这一典型范例。 具体的文章请参考张海军教授的文章(Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface http://dx.doi.org/10.1038/nphys1270)。还有一些功能可以用于计算QPI能谱(STM傅里叶变换谱)还有待用户自行测试。